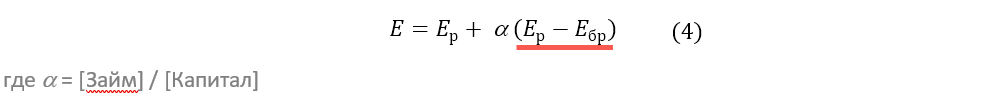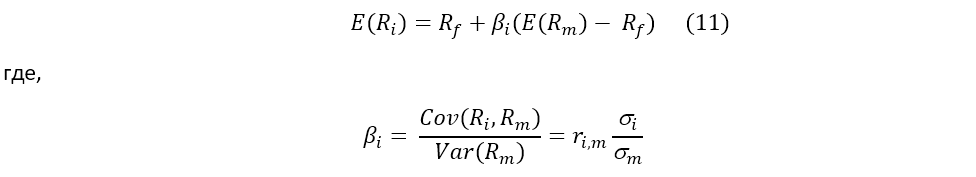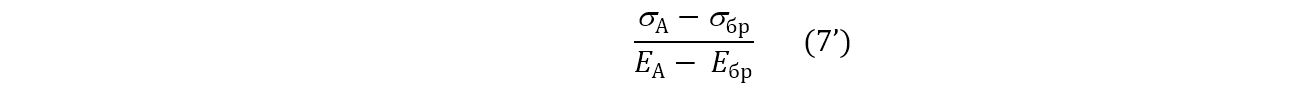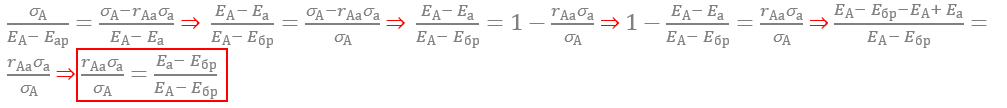Что имел ввиду Вильям Ф. Шарп?

В 1990 году Шарп, Марковиц и Миллер совместно получили Нобелевскую премию по экономике за изучение финансовых рынков и инвестиционных решений, основы которого были заложены в этой работе. САРМ сегодня является одной из двух широко распространенных моделей оценки активов (вторая – модель Гордона [1]).  

В своей работе Шарп опирается на несколько предпосылок, в объективности которых не мешает убедиться, ведь если некоторые из них содержат в себе определенные ограничения, то и сам метод следует применять с осторожностью.

Предпосылки модели САРМ:

• все инвесторы стремятся прирастить свой капитал;

• все инвесторы стремятся минимизировать уровень риска в погоне за приростом своего капитала;

• инвестор имеет возможность осуществлять безрисковые капвложения по безрисковой ставке;

• портфель капвложений является эффективным;

• индивидуальное капвложение входит в какой-либо эффективный портфель;

• влияние идиосинкразического, то есть не-систематического риска не принимается в расчет требуемой ставки доходности. Другими словами, эффективный портфель хорошо диверсифицирован.

Попробуем разобраться на основе вольного перевода оригинальной статьи Вильяма Форсайта Шарпа 1964-го года, почему возникла необходимость в предпосылках и каким именно образом они влияют на выводы Шарпа. Тем читателям, которые испытывают дефицит времени, можно порекомендовать обратиться сразу к заключительному разделу статьи.

«ОЦЕНКА КАПИТАЛЬНЫХ ВЛОЖЕНИЙ: ТЕОРИЯ РЫНОЧНОГО РАВНОВЕСИЯ С УЧЕТОМ РИСКА»[2]

Вильям Ф. Шарп, Финансовый журнал, №3, Сентябрь 1964

Одной из самых насущных проблем инвесторов по всему миру по мнению Шарпа являлось в то время отсутствие теории оценки капиталовложений (capital asset), учитывающей уровень риска. По имеющимся на тот момент взглядам ценообразование капиталовложений происходит в результате взаимодействия индивидуальных предпочтений инвесторов и основывается на предположении, что соотношение риск-премии и стоимости капиталовложений (а, следовательно, и их доходности) определяется рынком.

Рынок капиталовложений удобно рассматривать на примере Capital Market Line (CML), связывающей между собой риск и ожидаемую доходность. Как видно из Рисунка 1 рынок определяет «цену времени»[3] (pure interest rate, на пересечении CML и горизонтальной оси) и «цену риска»[4] – дополнительную доходность на единицу принятого риска. То есть инвестор может получить более высокую ставку доходности, чем «цена времени», только принимая соответствующий уровень риска. При этом рациональный инвестор, используя диверсификацию, может сформировать портфель с уровнем риска не больше, чем демонстрирует CML.

Шарп постулировал, что поведение инвестора описывается следующими предпочтениями: первое, инвестор стремится к росту своего капитала, второе, при прочих равных условиях инвестор выбирает капиталовложения с более низким уровнем риска. В результате кривая безразличия инвестора имеет наклон вправо [5] как на Рисунке 1 (здесь представлен упрощенный случай прямой линии, хотя в общем случае линия имеет форму кривой, имеющей общий наклон вправо).

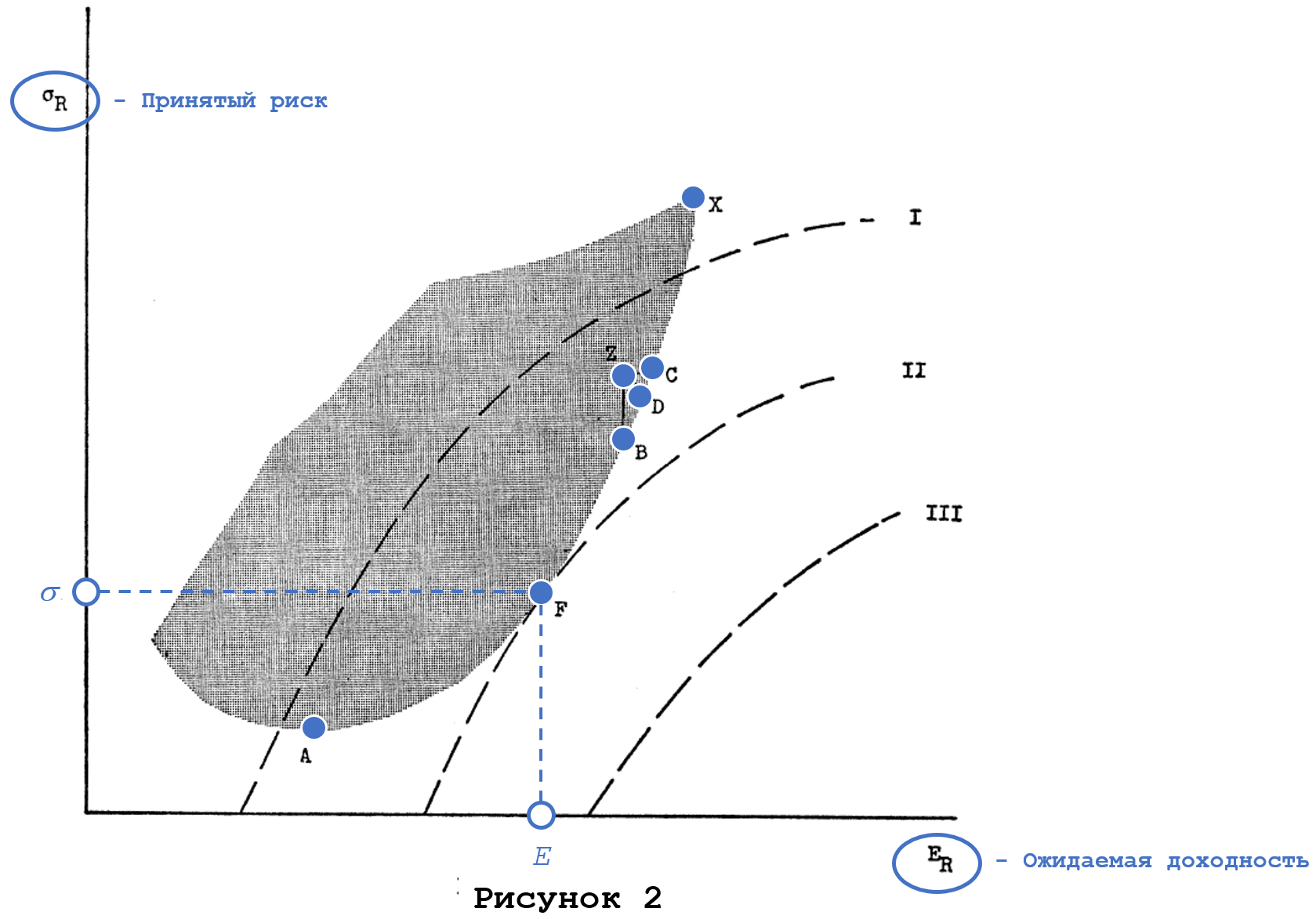
Уровень риска определяется волатильностью доходности капвложений, которая измеряется среднеквадратическим отклонением, то есть чем сильнее в прошлом наблюдался разброс доходности, тем выше риск. Доходность обозначается буквой r и характеризуется средним значением или ожидаемой доходностью, обозначаемой E (expected rate of return), значение которой показывает уровень доходности. Пара значений (среднеквадратическое отклонение -доходность) характеризует соотношение риск-доходность капвложения, поэтому множество альтернативных капвложений отражается на плоскости в виде точек с координатами: среднеквадратическое отклонение по вертикальной оси, доходность — по горизонтальной как на Рисунке 2 (серая закрашенная область в виде башмака).

Если отразить на плоскости все имеющиеся на рынке варианты капвложений (включая различные комбинации – то есть портфели) с определенной доходностью и уровнем риска, образуется некая фигура, например, закрашенная область в виде башмака на Рисунке 2, предположил Шарп. Из всех этих имеющихся вариантов инвестор выбирает наиболее эффективный.

Инвестор стремится получить максимальную доходность при минимальном риске, следовательно выбор инвестора можно назвать эффективным, если отсутствуют следующие альтернативные капвложения:

первое, с той же доходностью, но меньшим риском,

второе, с тем же риском, но более высокой доходностью,

третье, с более высокой доходностью и более низким риском.

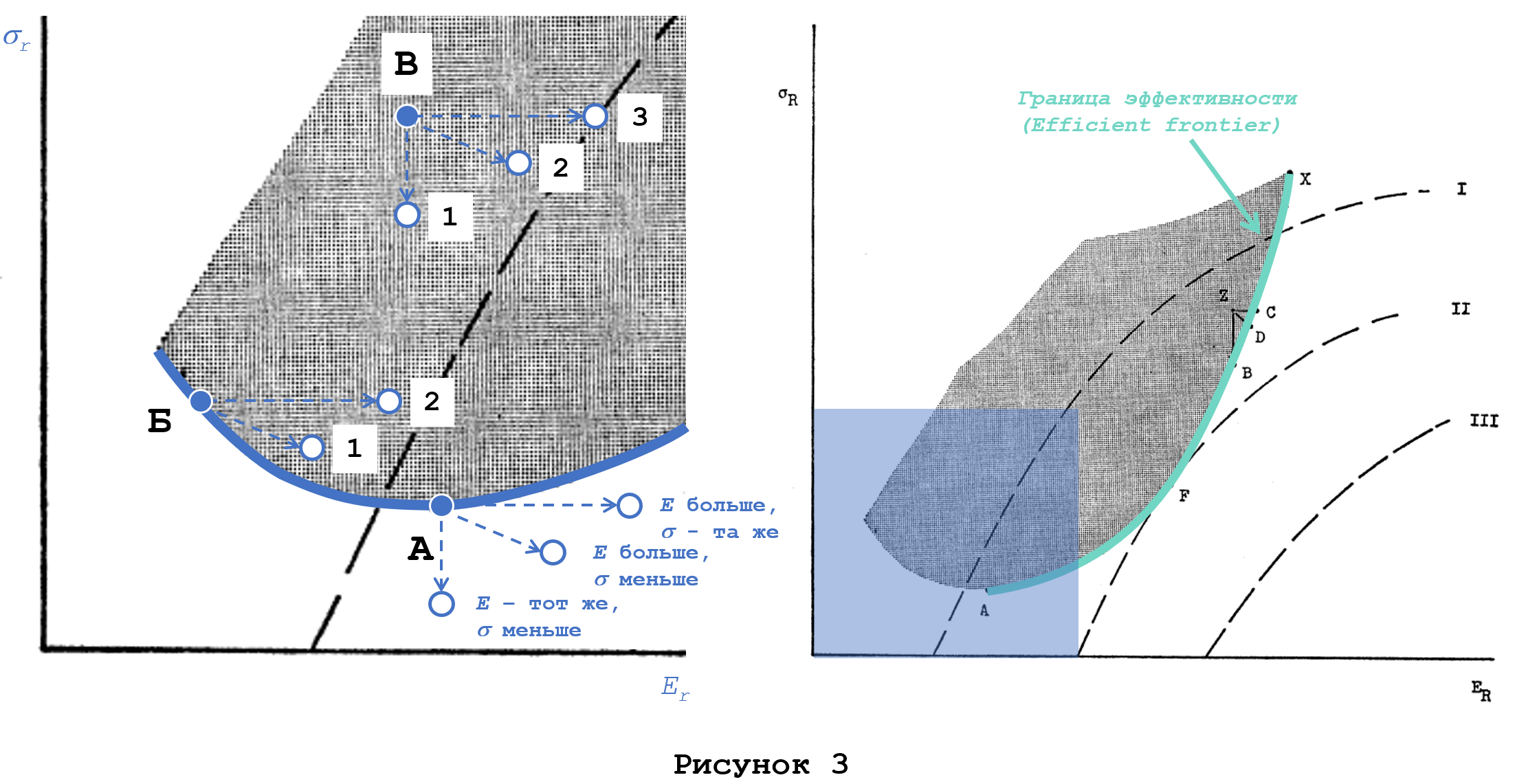
Как видно на Рисунке 3 точка А отвечает условиям эффективности, т.к. в рамках закрашенной области более эффективные точки отсутствуют (относительно точки Б есть два направления с более эффективными альтернативами, относительно точки В более эффективных направлений целых три). Нетрудно увидеть, что эффективные капвложения собрались на правой нижней границе закрашенной области – множества альтернативных капвложений (Рисунок 3 справа).

Кривая, на которой лежат эффективные варианты капвложений, имеет выгнутую форму и общий наклон вправо. Наклон именно вправо (а не влево) продиктован рассмотренными ранее предпочтениями инвесторов. Выгнутая форма кривой продиктована формулой уровня риска (стандартного отклонения) для портфеля из двух капвложений А и Б

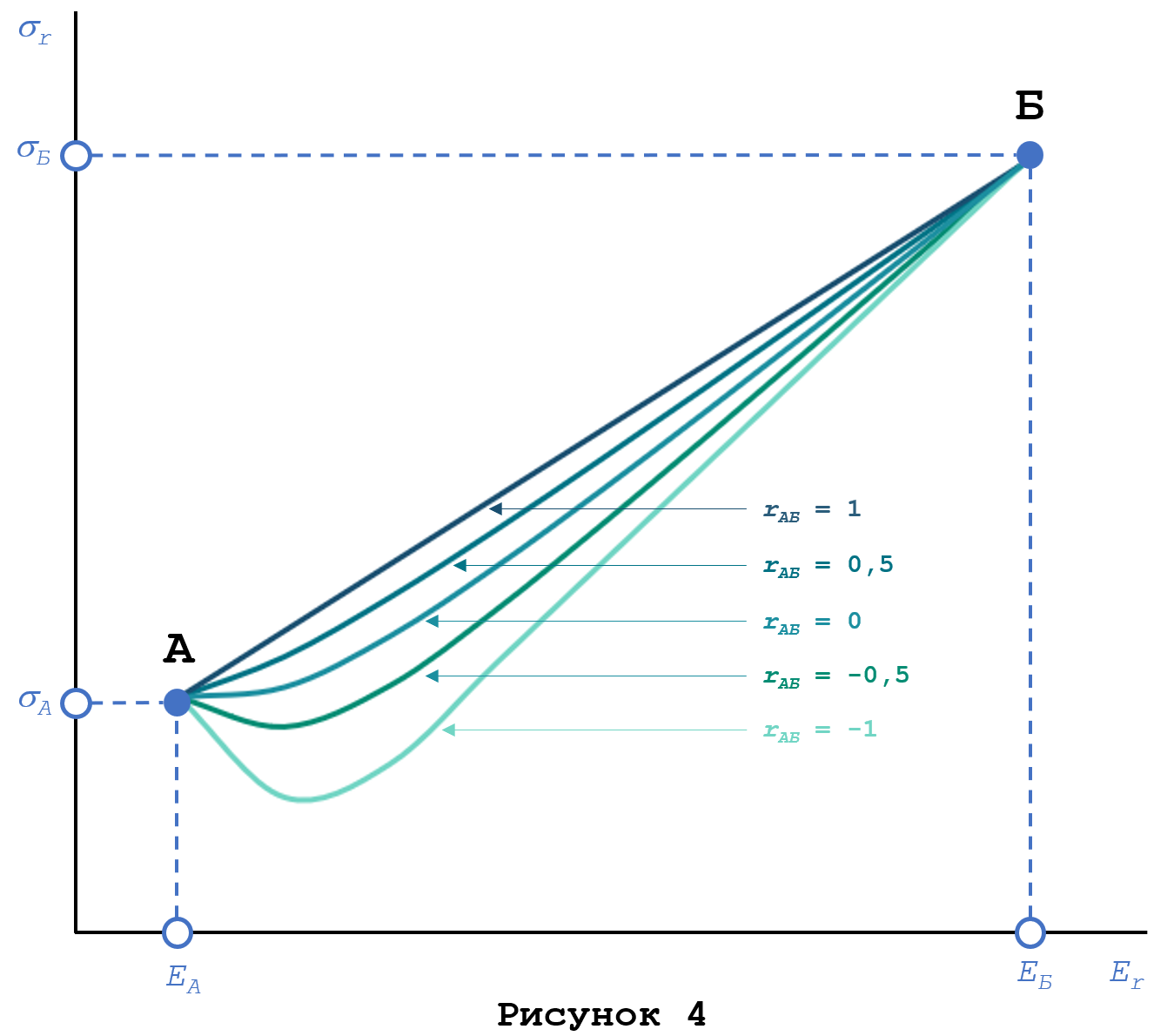
Из формулы (1) видно, что стандартное отклонение комбинации капвложений зависит от коэффициента корреляции доходности А и Б (подчеркнуто красным). Если коэффициент корреляции равен единице, то форма зависимости «риск-доходность» от пропорций капвложений А и Б в портфеле α : (1 — α) будет иметь вид прямой линии как на Рисунке 4. По мере изменения коэффициента корреляции прямая превращается в выгнутую кривую, а наиболее U-образную форму кривая принимает при коэффициенте корреляции равном -1. Наличие между активами сильной положительной корреляции (коэффициент корреляции = 1) встречается сравнительно редко, что и объясняет, почему граница области альтернативных капвложений на Рисунке 3 имеет выгнутую форму, а не прямую.

Вернемся к безрисковой ставке, которая лежит на пересечении CML с осью Er (Рисунок 1). Безрисковая ставка показывает чистую цену времени, поскольку к ней не примешивается никакая риск-премия. Инвестор почти всегда имеет возможность распределить свои капвложения между безрисковым активом [6] и активом с риском в пропорции α : (1 — α). Если доля капвложений в безрисковый актив «a» равна α, а в актив с риском (1 — α), тогда ожидаемая ставка доходности портфеля

Стандартное отклонение портфеля безрискового актива и актива с риском соответствует приведенной ранее формуле (1), но, учитывая, что стандартное отклонение безрискового актива равно нулю, под корнем остается только

Таким образом, ожидаемая доходность портфеля (2) и его среднеквадратическое отклонение (3) находятся в линейной зависимости от доли безрискового актива как показано на Рисунке 5 (зеленая линия).

На Рисунке 5 хорошо видно, что капвложения А и В уже нельзя назвать наиболее эффективным выбором, поскольку на зеленой линии находятся альтернативы как с большей доходностью E при том же риске, так и с меньшим риском при той же доходности. То есть, всегда можно найти такой актив F, что портфель капвложений, состоящий из безрискового актива и актива F, является наиболее эффективным выбором инвестора, предпочтением которого является минимизация риска при бόльшей доходности.

Имеется еще одна возможность – осуществление капвложений за счет займов [7]. В соотношениях (2) и (3) заимствование отразится в виде отрицательного значения α. То есть в таком портфеле безрисковый актив уже полностью отсутствует, все средства инвестора размещены в F и общий размер капвложений превышает капитал инвестора (превышение финансируется за счет займа). Это известное явление финансового рычага, при котором доходность на капитал растет пропорционально разнице между доходностью актива с риском и стоимостью займа (выделено красным в формуле 4). Чем больше величина займа по отношению к капиталу (соотношение которых выражается через α) тем выше прирост доходности на вложенный капитал инвестора

Аналогично присутствие займа выступает катализатором волатильности дохода – при падении доходности актива с риском F, доходность всего портфеля понизится в большей степени – с коэффициентом (1 + α).

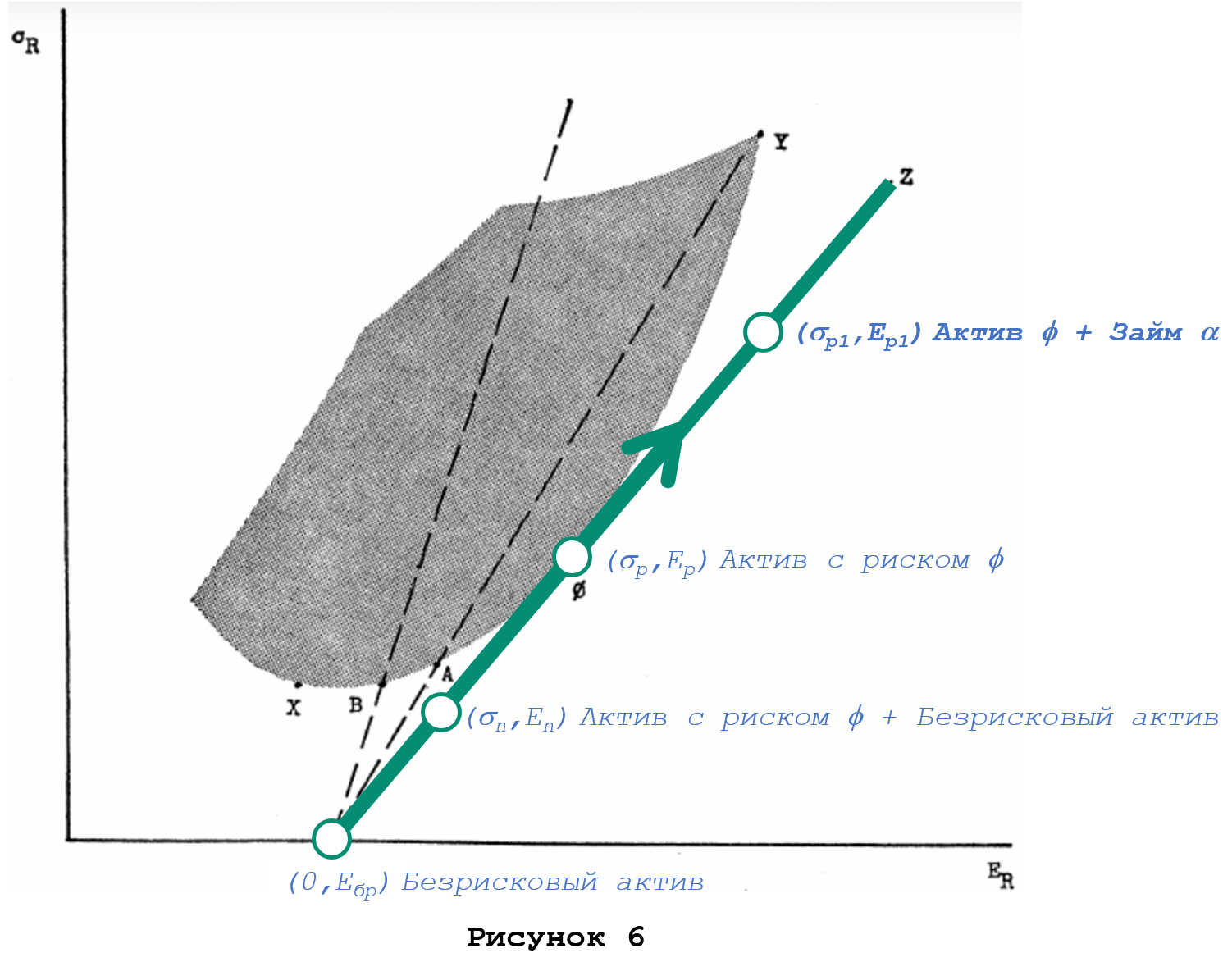
На графике эффект финансового рычага выглядит как продолжение зеленой линии вправо-вверх. Возможность заимствования снимает всякие ограничения по выбору соотношения риск-доходность, отвечающему предпочтениям инвесторов.

На Рисунке 6 видно, что зависимость между доходностью (горизонтальная ось) и риском (вертикальная ось) имеет линейный характер для всех эффективных капвложений, лежащих на линии Z. Какой же будет эта зависимость для других капвложений, не являющихся эффективными, задается вопросом Шарп?

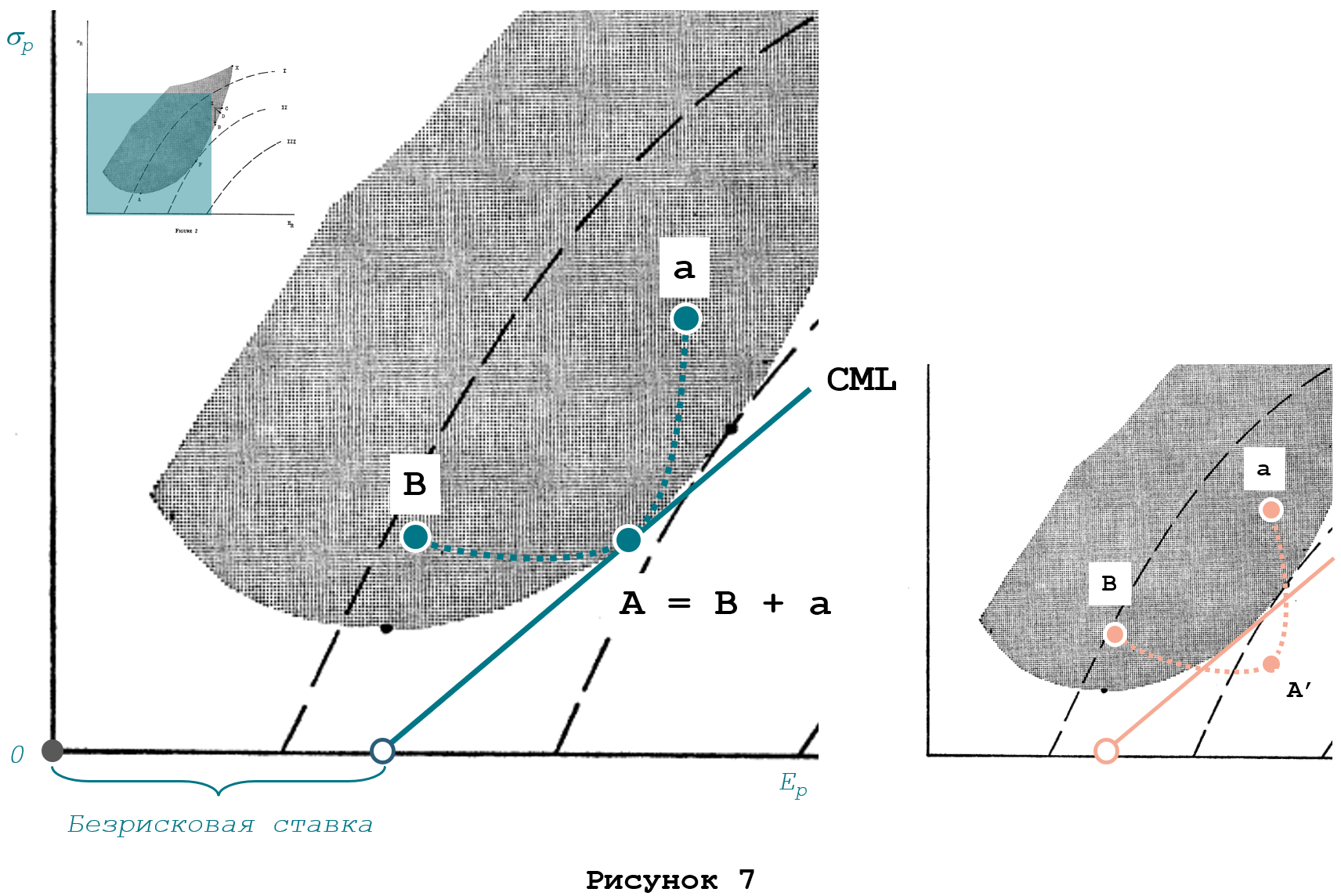
Для ответа на поставленный вопрос Шарп предлагает рассмотреть эффективный портфель А, включающий капвложение «а» и комбинацию (портфель) активов В (Рисунок 7). Кривая аАВ показывает альтернативные комбинации портфеля В и капвложения а, среди которых требованиям эффективности отвечает только портфель А, лежащий на CML.

Шарп утверждает, что кривая аАВ проходит к прямой CML по касательной не случайно, и действительно, если бы она пересекала CML, то тем самым обнаружился бы более эффективный портфель капвложений А’, что невозможно, т.к. А по определению лежит на самой границе эффективности (см. Рисунок 7 справа). Свойство кривой аАВ быть касательной к CML открывает возможность для вывода простой формулы зависимости риск-доходности между портфелем А и капвложением «а», не являющимся эффективным.

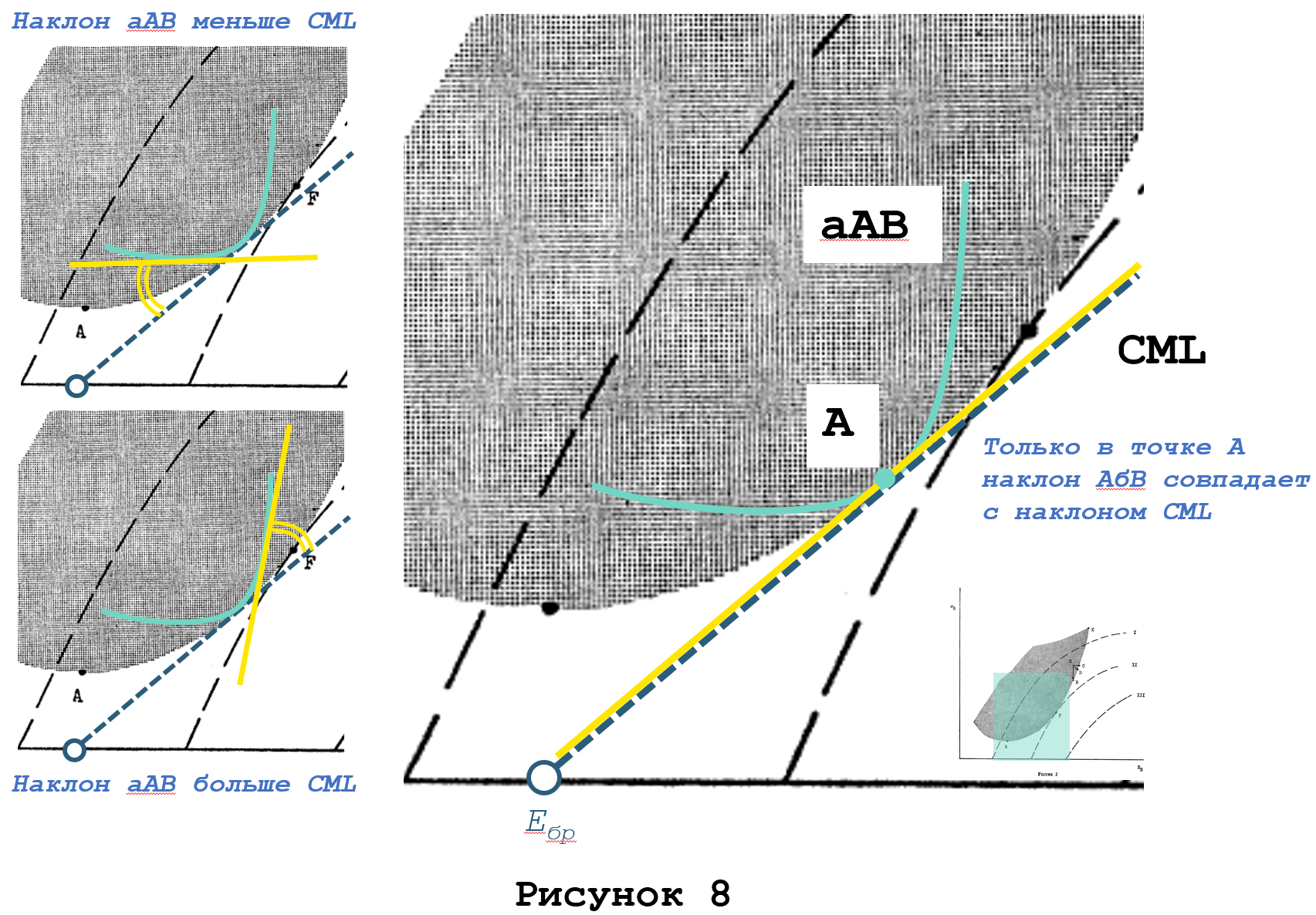
Действительно, в точке А сходятся кривая аАВ и прямая CML (Рисунок 8).

При этом наклон кривой аАВ в точке А подчиняется [8] соотношению

а наклон CML, как прямой линии, удовлетворяет следующему соотношению

Наклон кривой аАВ и CML совпадают в точке А, поэтому

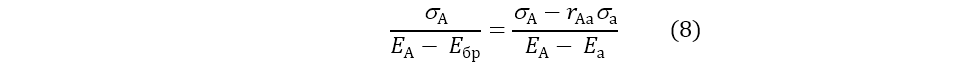
или [9]

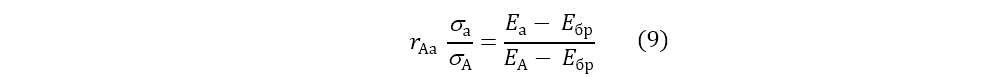
Таким образом, Шарп показал, что риск и доходность для всех капвложений, входящих в А, включая неэффективные, находятся между собой в линейной зависимости [10] так же, как и для эффективных портфелей.

Далее Шарп предлагает представить, как инвестор в разные моменты времени наблюдает доходности капвложения «а», входящего в портфель А. Соответствующие точки отражены на Рисунке 9, где по вертикальной оси отражена доходность капвложения «а» и по вертикальной – доходность всего портфеля, случайным образом разбросаны. Однако, как видно из Рисунка 9 будет наблюдаться закономерность, отражающая наличие линейной зависимости (9). Шарп назвал ту часть разброса, которая отвечает за проявление линейной зависимости, систематическим риском.

Взаимосвязь между доходностью конкретного капвложения и доходностью всего портфеля можно использовать в качестве предиктивной модели. То есть, если известны доходность и среднеквадратическое отклонение портфеля А, то любые входящие в него капвложения а должны иметь предсказуемые значения ожидаемой доходности E и среднеквадратического отклонения в соответствии с формулой (10). Отклонения от среднего значения, которые носят случайный характер, то есть не удовлетворяющие соотношению (9), отражают наличие не-систематического или иначе идиосинкразического [11] риска.

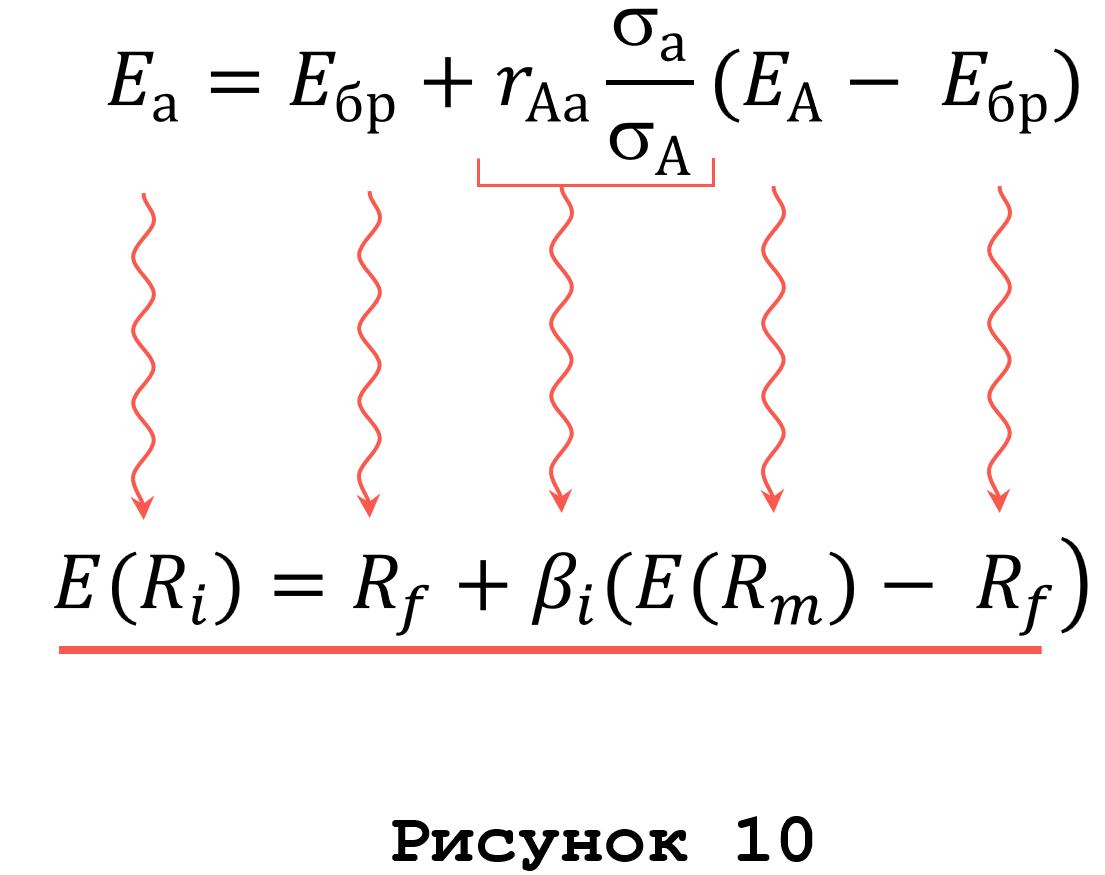
Путем несложных математических преобразований [12] приходим к другой форме записи соотношения (9)

которая, легко увидеть, соответствует формуле модели оценки капвложений САРМ

То, что ставки доходности всех эффективных портфелей коррелируют между собой, может означать, что все они находятся в зависимости от некоего общего для всех уровня экономической активности. Если это, верно, утверждает Шарп, тогда диверсификация портфеля позволяет избежать всех рисков кроме влияния экономических циклов. Более того, поскольку все другие виды рисков могут быть диверсифицированы, в расчет следует принимать только взаимосвязь между доходностью и общим уровнем экономической активности.

ПРЕДПОСЫЛКИ ШАРПА

В своей работе 1964 года Шарп установил простую связь между уровнем риска и уровнем доходности кавпложений. Его формула (11) взята на вооружение инвесторами всего мира, является основной методикой инвестиционного анализа в рамках таких курсов как МВА, CFA, СМА.

Остановимся на основных предпосылках [13], которые Шарп использовал, и, которые, следовательно, нужно всегда иметь ввиду, используя формулу САРМ:

• все инвесторы стремятся прирастить свой капитал;

• все инвесторы стремятся минимизировать уровень риска в погоне за приростом своего капитала;

• инвестор имеет возможность осуществлять безрисковые капвложения по безрисковой ставке;

• инвестор имеет возможность осуществлять займы по безрисковой ставке;

• влияние идиосинкразического, то есть не-систематического риска не принимается в расчет требуемой ставки доходности. Другими словами, портфель в формуле (11) хорошо диверсифицирован;

• портфель капвложений А в формуле (11) является эффективным;

• индивидуальное капвложение «а» в формуле (11) входит в эффективный портфель А.

Действительно, в подавляющем большинстве случаев за редким исключением, когда выгоды выражаются в различных эстетических и эмоциональных прелестях, инвесторы преследуют прагматические цели.

Инвестор имеет возможность осуществлять безрисковые капвложения по безрисковой ставке

Современное определение безрисковой ставки утверждает [14], что это теоретическая ставка доходности вложений в активы с нулевым риском. Другими словами, безрисковая ставка является воображаемой процентной ставкой доходности, которую инвестор ожидает получить от абсолютно безрисковых вложений. Реальная величина безрисковой ставки может быть рассчитана, например, путем вычитания из доходности государственных обязательств ставки инфляции. Однако, имеется ли волатильность у такой ставки доходности? Для модели САРМ это важно, так как в своих рассуждениях Шарп ставит знак равенства между отсутствием риска и нулевым значением среднеквадратического отклонения.

Что, если среднеквадратическое отклонение «безрисковой» ставки не равно нулю?

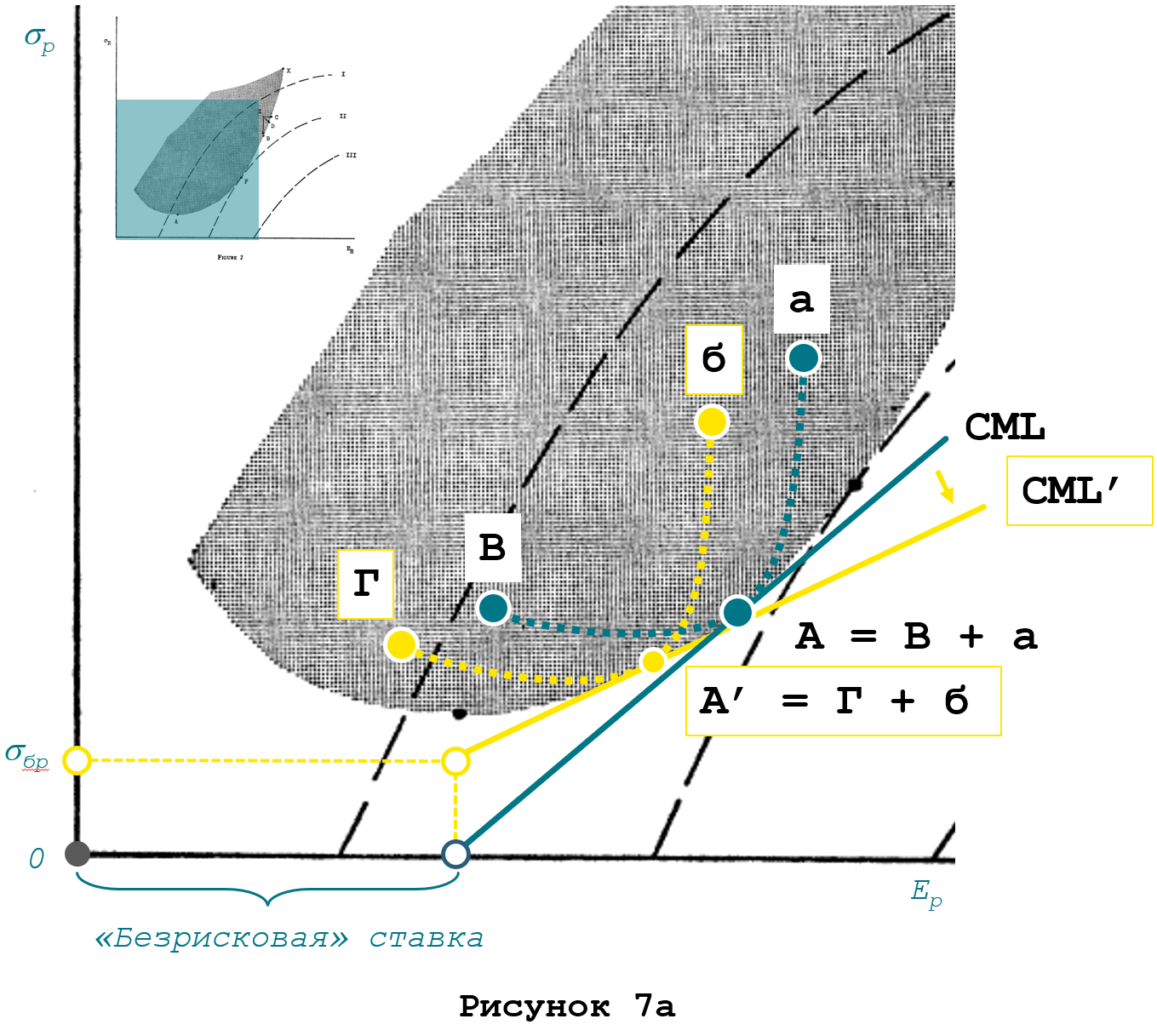
Это приведет к изменению вида линии CML, она трансформируется в CML’ как на рисунке 7а (желтая линия). Нижняя точка линии CML’ окажется теперь над горизонтальной осью, наклон линии вправо увеличится. Это означает, что эффективный выбор инвестора будет включать другой актив на границе эффективности – А’. Такое изменение пока еще не приводит к искажению дальнейших рассуждений Шарпа, так как свойство кривой бА’Г быть касательной к CML’ не утрачивается.

Какой будет формула линии CML’? Она изменится.

Наклон линии CML’ удовлетворяет соотношению

следовательно, равенство (8) переходит в равенство (8’)

а основная формула САРМ (10) преобразуется в

Как видно из (10’) существенно поменялось выражение «беты», которое включает теперь стандартное отклонение «безрискового» актива

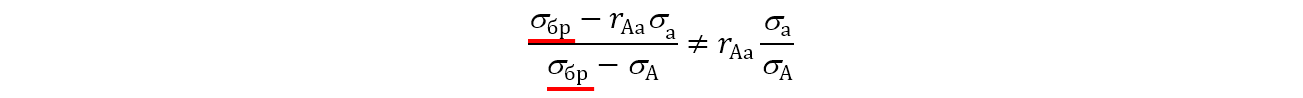
Действительно, доходность даже наименее рискованных активов не лишена волатильности. Так, за период 2014-2019 гг. среднеквадратическое отклонение доходности ОФЗ составило 4%. Расчеты показывают, что при такой волатильности «безрискового» актива отклонение от теоретической «беты» может колебаться в диапазоне 0,5-1 единиц. Другими словами, неопределенность при величине риск премии 10% составляет 5 – 10 пп.

Инвестор имеет возможность осуществлять займы по безрисковой ставке

Ценообразование при предоставлении займов осуществляется по следующей формуле

+ «безрисковая ставка»

+ «риск премия в соответствии с уровнем кредитного риска заемщика»

+ «себестоимость предоставления займа»

+ «норма прибыли займодавца».

Легко увидеть, процентная ставка по займу не может равняться безрисковой ставке даже для высококлассных заемщиков, поскольку даже при нулевой премии за кредитный риск процентная ставка будет превышать безрисковую на величину себестоимости и нормы прибыли займодавца.

В цепи логических рассуждений Шарпа возможность осуществлять займы по безрисковой ставке отвечает за продление линии CML вправо-вверх и выполнение ею роли касательной (см. Рисунок 6). Тот факт, что линия CML проходит по касательной к линии аАВ (см. Рисунок 7), позволяет утверждать равенство

из которого путем тождественных преобразований вытекает основная формула САРМ

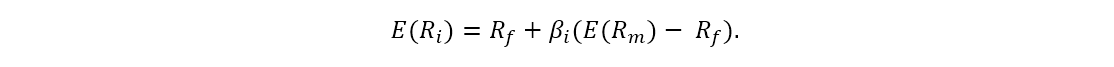
Справедливо ли будет утверждение, что CML проходит по касательной к линии аАВ, если инвестор не имеет возможности осуществлять займы по безрисковой ставке?

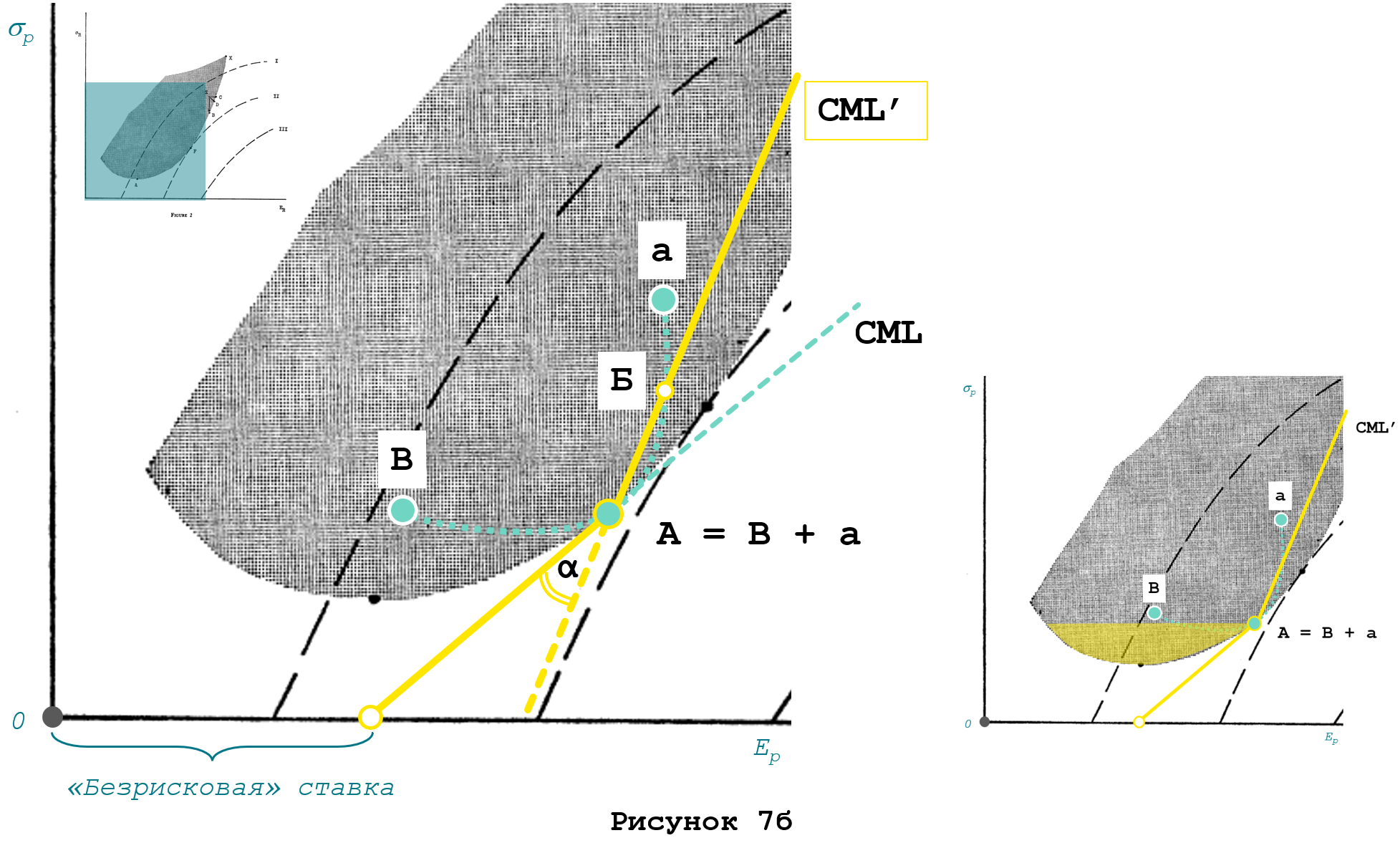
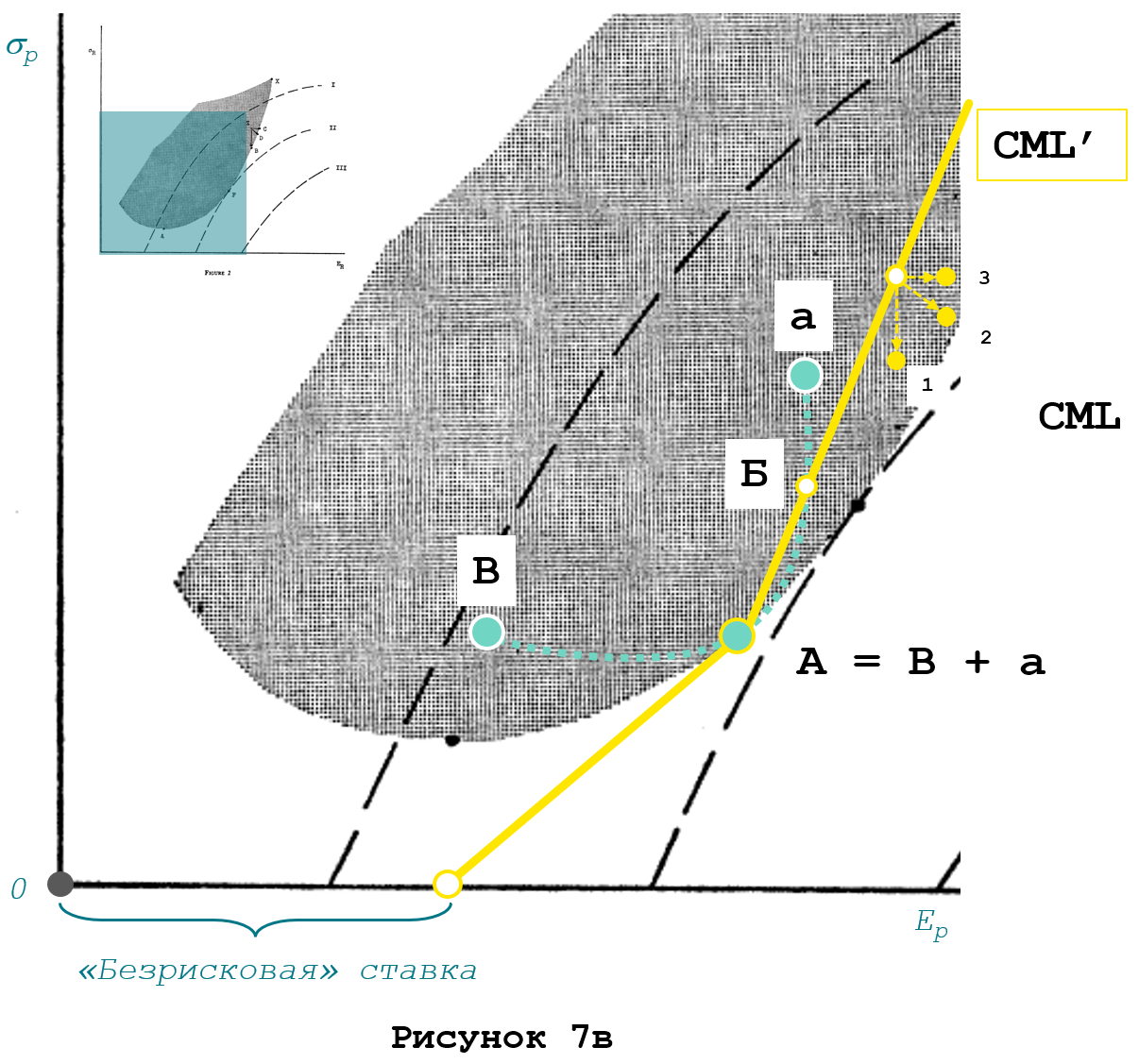
Линия CML’ переламывается в точке А, как видно на Рисунке 7б, так как процентная ставка, по которой осуществляются займы больше, чем безрисковая ставка. Говоря математическим языком, линия CML’ имеет «точку излома» в точке А, в которой она имеет две касательные, пересекающиеся под углом α. В точке А линия аАВ проходит только по одной из двух касательных, при этом вторую она пересекает в точке Б.

На поставленный вопрос можно ответить «да», справедливо, но только для тех активов, риск-доходность которых меньше, чем у актива А (рисунок 7б, справа, желтая область).

Если принять во внимание, что заимствование осуществляется по более высокой ставке, оказывается, что формула САРМ справедлива не для всех активов.

Выполнение CML роли касательной также является основанием для снятия ограничений по выбору соотношения риск доходность (см. Рисунок 6), поскольку осуществление увеличение объема инвестиций за счет займов дает возможность продлить CML до бесконечности.

Будут ли капвложения, лежащие на линии CML’, эффективными, если ставка, по которой можно осуществлять займы, выше безрисковой?

Правее точки А линия CML’ забирает вверх, следовательно возникают более эффективные альтернативы (рисунок 7б: 1, 2 и 3) с меньшим риском при том же уровне доходности, то есть, CML’ не является кривой безразличия для инвесторов, использующих займы.

Если принять во внимание, что заимствование возможно только по более высокой ставке, чем безрисковая, окажется, что формула САРМ справедлива не для всех активов и существуют эффективные капвложения, лежащие правее CML.

Портфель А хорошо диверсифицирован

Шарп рассматривает взаимосвязь систематического риска и доходности, то есть предполагается, что не-систематический риск полностью исключен, значит, портфели активов хорошо диверсифицированы. Другими словами, портфель активов, который не диверсифицирован не может удовлетворять формуле САРМ.

Выделяют следующие признаки хорошей диверсификации:

• доля одного актива не слишком большая;

• не слишком мало активов;

• не слишком большая доля одной отрасли экономики.

На практике используют какой-либо фондовый индекс – индекс МосБиржи, например. База расчета индекса МосБиржи включает около 40 ценных бумаг эмитентов из разных отраслей экономики:

В расчете индекса МосБиржи более 80% занимают три отрасли, причем доля нескольких активов в базе расчета превышает 10%. Если бы на такой базе расчета был сформирован инвестиционный портфель, его нельзя было назвать хорошо диверсифицированным.

Ставка доходности, рассчитанная с применением САРМ, в таком случае включает в себя не-систематические риски трех наиболее значимых для индекса МосБиржи отраслей. Другими словами, в расчете ставки доходности актива, например, в транспортной отрасли будут учтены риски нефтегазовой, металлургической отраслей и финансового сектора экономики.

Портфель капвложений А является эффективным

Вспомним, что портфель можно считать эффективным, если отсутствуют следующие альтернативные капвложения:

• с той же доходностью, но меньшим риском,

• с тем же риском, но более высокой доходностью,

• с более высокой доходностью и более низким риском.

Другими словами, портфель активов должен лежать на границе эффективности, чтобы считаться эффективным. Чтобы убедиться в том, что индекс МосБиржи лежал бы на границе эффективности необходимо явным образом убедиться, что ни один другой актив или портфель активов не обладает:

• той же доходностью, но меньшим риском,

• тем же риском, но более высокой доходностью,

• более высокой доходностью и более низким риском.

Если индекс МосБиржи не лежит на границе эффективности (как в точке Г на Рисунке 7г), то у линии аАВ исчезает свойство быть касательной к линии CML. Важность данного свойства имеет большое значение, так как только при таком условии возможен вывод формулы (11). Необходимо доказательство эффективности индекса МосБиржи, чтобы оправдать его применения в формуле (11).

 

Индивидуальное капвложение «а» в (11) входит в эффективный портфель

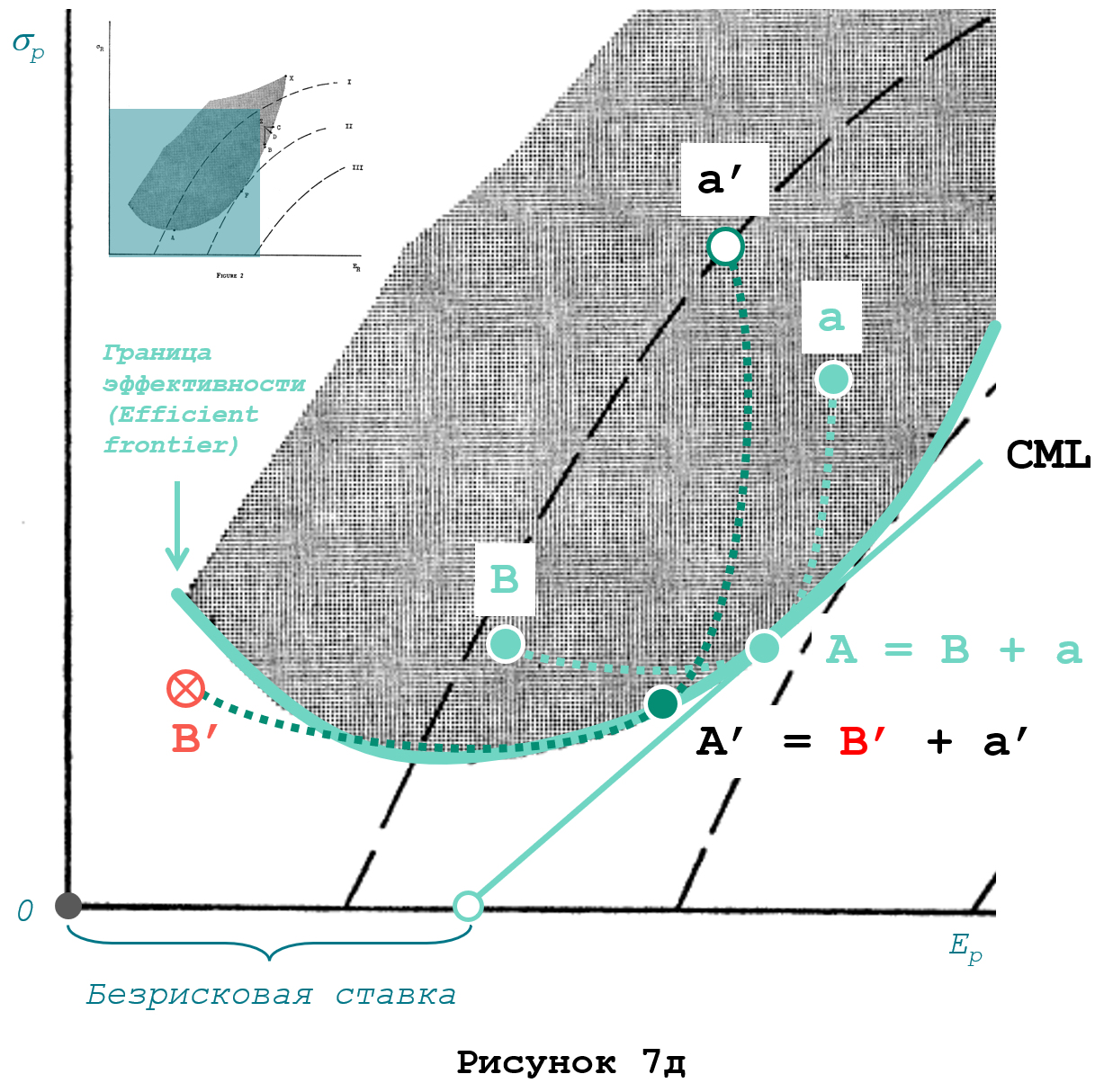
Расчеты САРМ справедливы только для тех активов, которые входят в какой-либо эффективный портфель. Теоретически для любого актива а’ можно подобрать такой актив В’, что их комбинация А’ = а’ +В’ окажется эффективным портфелем (то есть будет лежать на границе эффективности, как портфель А). Однако, может оказаться, что требуемый актив В’ лежит за пределами области реальных активов (см. Рисунок 7д).

Применение САРМ для актива «а» в таком случае не покажет объективного результата.

Послесловие

Одним из важнейших ограничений применения САРМ является игнорирование идиосинкразического риска. Другими словами, ставка доходности, полученная по модели Шарпа, не отражает индивидуальные риски актива. Если нужно рассчитать требуемую ставку доходности актива c учетом его индивидуальных рисков, с помощью САРМ этого не сделать.

Для того, чтобы получить объективный результат с применением САРМ, нужно быть внимательным к деталям. В принципе, использование любого инструмента в реальной жизни возможно только в определенных границах, за пределами которых инструмент перестает выполнять свою задачу. Так же характеристики некоторых активов могут выходить за границы применения модели Шарпа, что приведет к искажению результата.

Так, использование финансовых индексов в качестве эффективного портфеля приводит к тому, что требуемая ставка доходности учитывает идиосинкразические риски имеющих наибольший вес в индексе отраслей экономики, которые на самом деле не имеют отношения к рассматриваемому активу, так как база расчета финансовых индексов может быть не диверсифицирована, как например в индексе МосБиржи. Это приводит к неконтролируемому искажению величины риск-премии.

Другая особенность модели САРМ создает существенную неопределенность конечного результата, если «безрисковая» ставка обладает волатильностью как, например, происходит в действительности со ставкой ОФЗ – необходимо с осторожностью подходить к выбору безрисковой ставки, чтобы получить надежный результат применения САРМ.

Наиболее сложными с точки зрения контроля надежности результатов являются предпосылки об эффективности портфелей, ведь, если они не выполняются, формула САРМ вообще перестает работать.

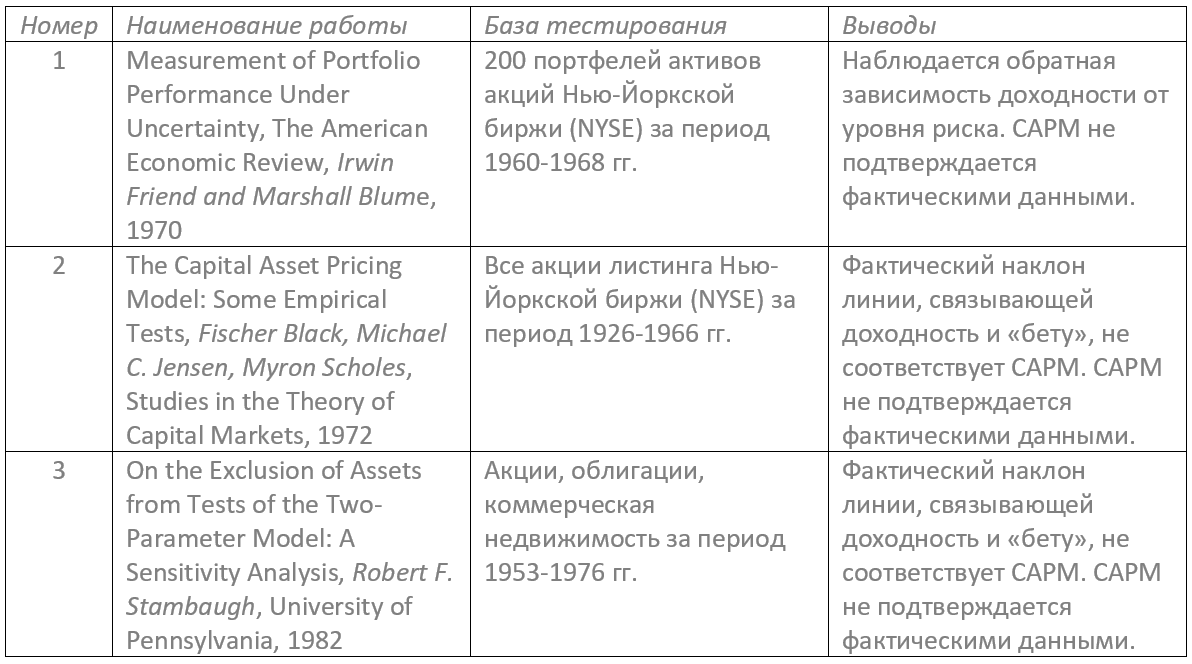
В работах иностранных авторов нередко встречается мнение об отсутствии подтверждений САРМ, полученных в ходе тестирования на основе фактических данных.

Наличие большого числа неочевидных предпосылок создает благоприятную почву для сомнений в применимости САРМ на практике и, как было показано, не без оснований. Практическое применение модели сталкивается с необходимостью внимательного контроля за соблюдением границ ее применения:

• безрисковая ставка практически лишена волатильности;

• рыночный портфель является эффективным;

• рыночный портфель хорошо диверсифицирован;

• доходность рассматриваемого актива меньше, чем доходность рыночного портфеля;

• доходность рассматриваемого актива не должна обладать слишком большой волатильностью;

• финансирование портфеля осуществляется только за счет собственных средств.

[1] чтобы быть справедливым — модель Гордона-Шапиро.

[2] материал подготовлен на основе статьи Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, William F. Sharpe, The Journal of Finance, Vol. XIX, No. 3, 1964. Используются иллюстрации непосредственно из данной публикации.

[3] безрисковая ставка.

[4] риск-премия.

[5] если бы инвесторы предпочитали капиталовложения с бόльшим уровнем риска и меньшей доходностью, наклон кривой был влево.

[6] безрисковый актив – это актив, вложение в который приносит постоянную ставку доходности, то есть не обладающую волатильностью.

[7] предполагается, что заимствование осуществляется по безрисковой ставке.

[8]

[9]

[10] данная зависимость действительно носит линейный характер, так как выражение не содержит переменных, возведенных в степень, или произведений переменных.

[11] идиосинкразический риск – вид риска, присущий только конкретному активу, как, например, конкретной компании, определенной отрасли или классу капвложений, например, ипотечные облигации. В отличие от систематического риска идиосинкразический риск может быть диверсифицирован. (https://www.investopedia.com/terms/i/idiosyncraticrisk.asp)

[12]

[13] другие предпосылки САРМ: инвестор не может влиять на цену; инвестор может получать займы по безрисковой ставке; отсутствуют транзакционные издержки; инвестор имеет такие же предпочтения и ожидания как другие; инвестору доступна такая же информация как другим.

[14] https://www.investopedia.com/terms/r/risk-freerate.asp#:~:text=The%20risk%2Dfree%20rate%20of%20return%20is%20the%20theoretical%20rate,a%20specified%20period%20of%20time.